How fat is the cat …… and is it macroscopic?

29th May 2013

MPQ Theory Seminar, Lucas Clemente

bit.ly/wed-macro or on github

Why care about cats?

Quantum Measurement Problem: Wave function collapse

Look for violations of QM:

Experiments

Matter-wave interferometry

SQUIDs

Bose-Einstein Condensates

Opto- & Magnetomechanics

Are they macroscopic?

Macroscopicity

Behavior is neither
classical, nor an
accumulated quantum effect.Think Cooper pairs in a superconductor.

Idea: Use effective number of particles. The smallest system size so that quantum mechanics explains the behavior. Think Neff = 2 for Cooper pairs.
Call a system macroscopic if effective size is linear Neff = $\mathcal O$ (N). I.e. all particles need to be described quantum mechanically.

Examples:

GHZ state: Neff = N, macroscopic

Cooper pair: Neff = 2, microscopic

Measures for Neff

Disconnectivity

Two Measures: (not strictly Neff)

Extensive difference $\Lambda$: difference of states vs reference value (e.g. $\Delta \Phi / \Phi_0$)

Disconnectivity D: degree of entanglement, possibly reduced entropy

Examples:

GHZ State of N particles: D = N

C60: D ≈ 106

Atomic ensembles: D ≈ 107

SQUIDs: D ≈ 1010

DSC Measure

Idea: Compare realistic (e.g. BEC) ↔ GHZ states

$$\ket{\psi} = \frac{1}{\sqrt{K}} \left( \ket{0}^{\otimes N} + \ket{\epsilon}^{\otimes N} \right)$$ where $\left| \braket{0}{\epsilon} \right|^2 = 1 - \epsilon^2$.

Through decoherence rate / max distillation:

$$N_{eff} = N \epsilon^2$$

BM Measure

Can a state improve phase estimation in interferometry?

Let $\ket{\psi(t)} = e^{-i H t / \hbar} \ket{\psi}$ and
$\theta(\ket{\psi}) :=$ time to reach orthogonal state.

Observe that $\theta(\ket{\psi}) \ll \theta(\ket{0}), \theta(\ket{1})$. Think small oscillations in an interference pattern.

Define the effective particle number $$N_\text{eff} = \left[ \frac{\theta(\ket{0}) + \theta(\ket{1})}{\theta{\ket{\psi}}} \right]^2$$

Examples:

C60: N ≈ 5

SQUIDs: N ≈ 33

Optomechanical $\ket{0} + \ket{1}$: N = 1 (?)

KWDC Measure

Divide $\ket{0} + \ket{1}$ into maximal number (n) of subsystems, so that measuring one we can distinguish the states with precision $\delta$.

Define effective size Neff = n.

Here, macroscopic = locally distinguishable

MAvD Measure

How many single-particle operations do we need to apply to get from $\ket{0}$ to $\ket{1}$?

  1. Start with $\mathcal H_0 = \operatorname{span} \{ \ket{0} \}$
  2. Define $\mathcal H_i$ by applying all possible single particle operations on $\mathcal H_{i-1}$
  3. Write $\ket{1} = \sum_i P_i \ket{1} = \sum_i \lambda_i \ket{v_i}$
  4. Effective size $\avg{N} = \avg{\sum_i i \ket{v_i} \bra{v_i}}$

Examples:

GHZ: Neff = N

Superconducting qubit: Neff ≈ 1

Many photon states: Neff = 1

Fisher Information

Fisher Information: expected value of the observed information.

Inverse of Cramer-Rao-Bound, "key resource" for metrology.

Implicit form: $$(ds)_\text{Bures} = \frac{1}{2\hbar} \sqrt{\mathcal F(\rho, H)} dt$$

For pure states: $$\mathcal F(\psi, H) = 4 \left[ \langle H^2 \rangle - \langle H \rangle^2 \right]$$

Let $A = \sum_i A_i$ be a locally acting operator with $||A_i|| = 1$. $$N_\text{eff}^F = \operatorname{max}_A \mathcal F(\rho, A) / (4 N)$$

Better measure: relative Fisher information $$N_\text{eff} = \frac{2 N_\text{eff}^F(\ket{\psi})}{N_\text{eff}^F(\ket{0}) + N_\text{eff}^F(\ket{1})}$$

Common Problems

NH Measure

… call a quantum system the more macroscopic the better its experimental demostration rules out a minimal modification of quantum mechanics …

Minimal Extension of QM

All extensions classicalize the system:

$$\partial_t \rho_N = [H, \rho_N] / i \hbar + \mathcal L_N \rho_N$$
  1. Invariant under Galilean trafo
  2. Leave exchange symmetry unaffected
  3. Innocent bystander condition Adding an uncorrelated system leaves reduced state unchanged.
  4. Scale invariant with respect to CM

For a single particle (using Holevo 1993):

$$\mathcal L_1 = \frac{1}{\tau} \left[ \int d^3 s d^3 q g(s, q) W(s, q) \rho W^\dagger (s, q) - \rho \right ]$$

where $W(s, q) = \exp [ i/\hbar (P s - q X) ]$.

$g(s, q)$ a positive, isotropic, normalized phase space distribution with standard deviations $\sigma_s$, $\sigma_q$.

Matrix elements of $\rho$ that are larger than $\sigma_s$, $\sigma_q$ decay with $\tau$.

Using the other conditions we get, for a massive object (M, mass density $\varrho$) approximated by a single particle:

$$\frac{1}{\tau} = \frac{1}{\tau_e} \frac{1}{m_e^2} \int d^3 s d^3 q g_e(s, q) |\tilde \varrho(q)|^2$$ $$g(s, q) = \frac{\tau M^3}{\tau_e m_e^5} g_e(s M/m_e, q) |\tilde \varrho(q)|^2$$ Note that for an elementary particle $\tau = \tau_e (m_e/m)^2$

Different experimental bounds:

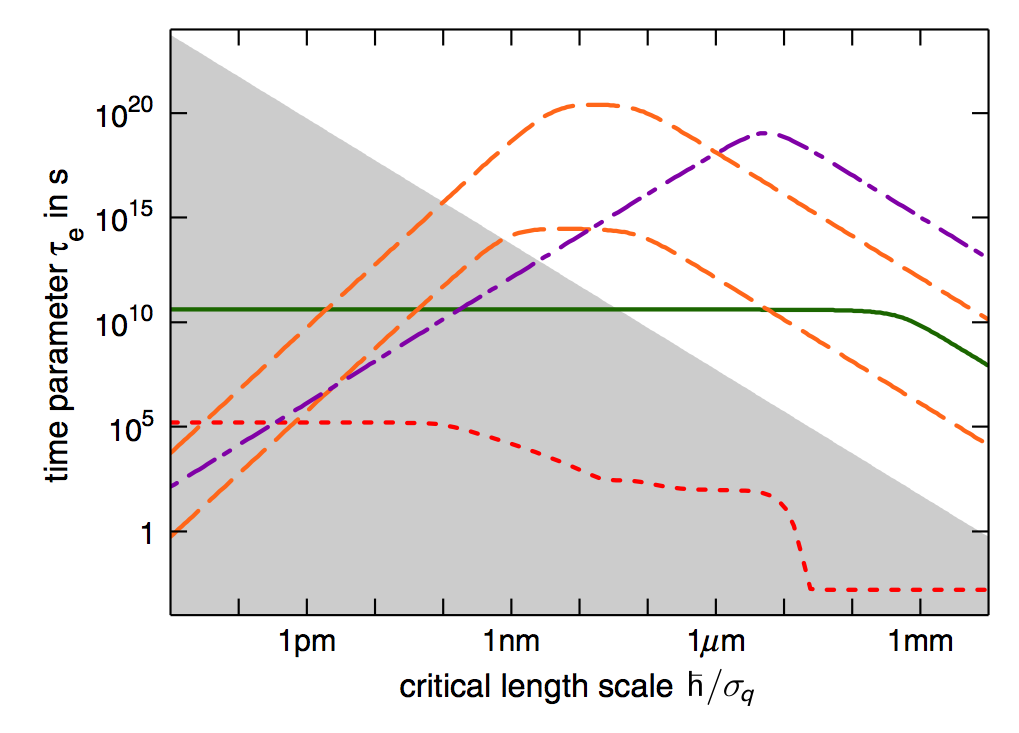
Define macroscopicity as

$$\mu = \log_{10} \left( \frac{\tau_e}{1~\text{s}} \right)$$ For double-slit-like experiments: $$\mu = \log_{10} \left[ \frac{1}{|\ln f|} \left(\frac{M}{m_e}\right) \frac{t}{1~\text{s}} \right]$$ where $f$ is the visibility.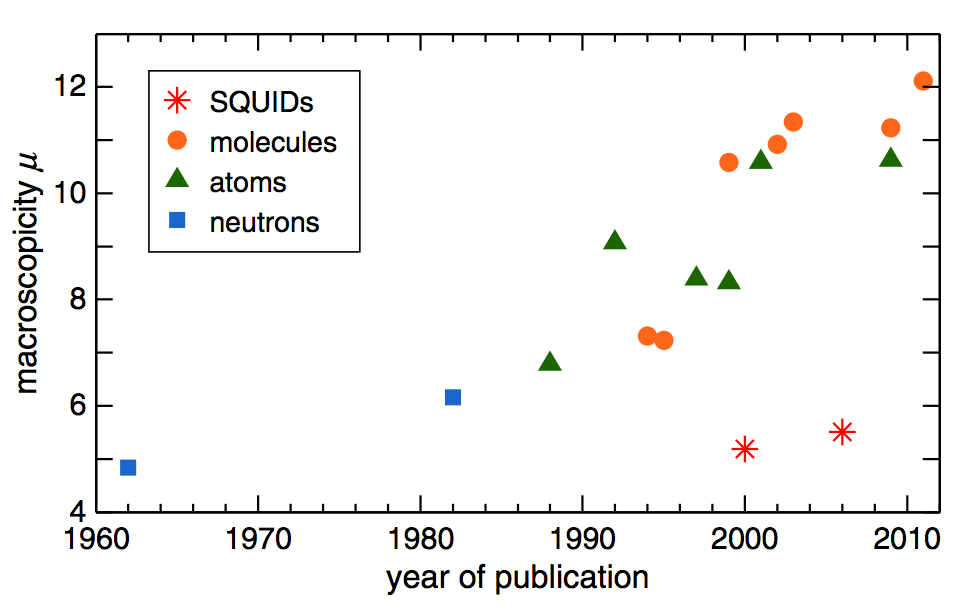
Experiment μ
Oscillating micromembrane 11.5
Hypothetical large SQUID 14.5
Talbot-Lau interference at 105 amu 14.5
Satellite atom (Cs) interferometer 14.5
Oscillating micromirror 19.0
Nanosphere interference 20.5
Talbot-Lau interference at 108 amu 23.3
Schrödinger gedanken experiment ~57

Lessons learned

My gut reaction is that while the idea in this paper is a clever one, it is facing in an irrelevant direction. Rather than referring to quantum mechanics in its formulation, macroscopicity should instead reflect our ‘common-sense’ intuition of the difference between an electron being in an indefinite state and a cat being in an indefinite state. - Tony Leggett

Subjective stuff is hard!

Approaches: particle number / experimental effects

What insight did we gain?

Thank you!again, bit.ly/wed-macro