Macro
realism

MPQ theory wednesday seminar by Lucas Clemente

clemente.io/macrorealism — github

2015-01-14

This is joint work with Johannes.

The paper will be on the arxiv soonish :)

Schrödinger's cat!

What else?

Macroscopic superpositions

Molecules, atomic gases, superconducting qubits, nanomechanics, …

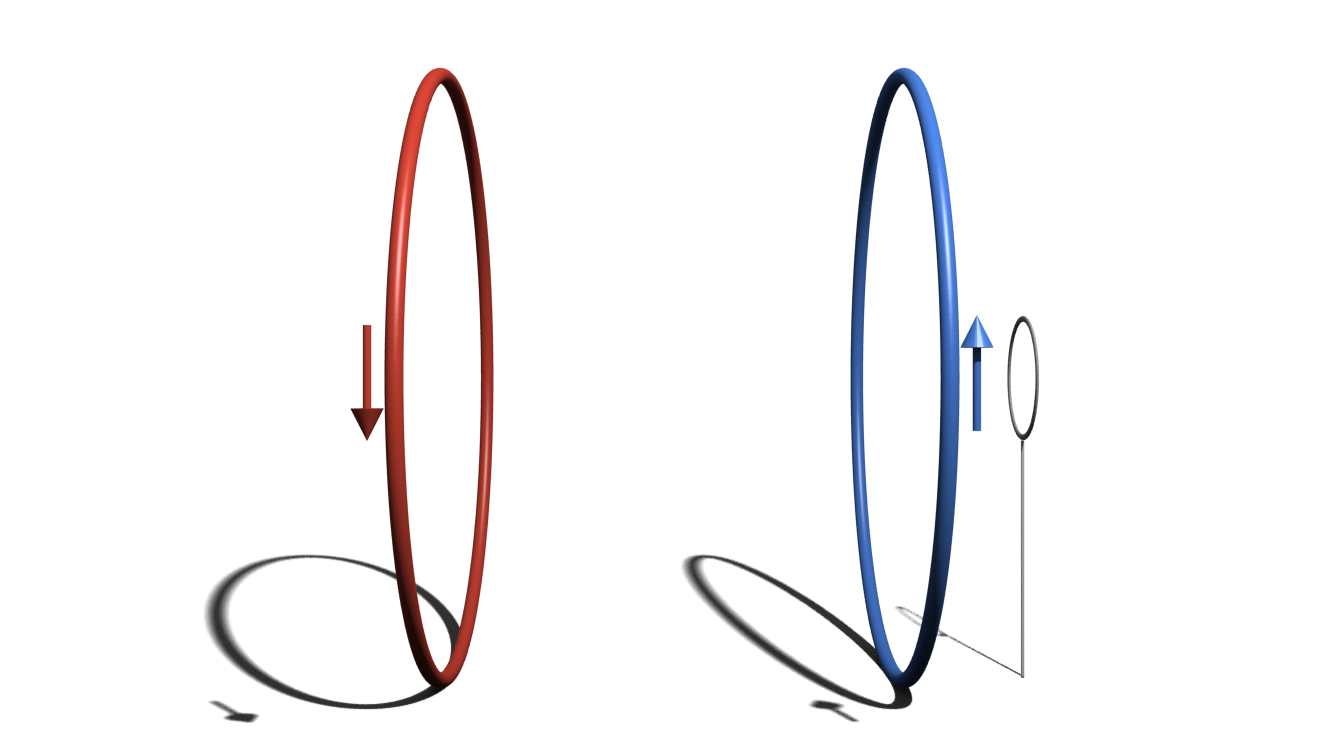
Macroscopic Realism

Legget, Garg 1985

The world view that macroscopic physical properties
are independent of measurements.

Conditions for Macrorealism

1. Macrorealism
per se

A macroscopic object occupies
a definite macrostate at all times.

Conditions for Macrorealism

2. Noninvasive Measurements

It is possible to measure the state
without changing it (or the future evolution).

Conditions for Macrorealism

3. Arrow of time

4. Freedom of choice

Mathematical formulation?

Legget-Garg Inequalities

A simple experiment

Macro-observable $Q = \pm 1$

Measurements at times $t_0, t_1, t_2$ with outcomes $Q_i$

Correlations $C_{ij} \equiv \langle Q_i Q_j\rangle = p_{++} + p_{--} - p_{+-} - p_{-+}$

Macrorealism =

Joint Probability Distribution

$$P(Q_0, Q_1, Q_2)$$

at times $t_0$, $t_1$, $t_2$

$$C_{01} = [P(+,+,+) + P(+,+,-)] \\+ [P(-,-,+) + P(-,-,-)] \\- [P(+,-,+) + P(+,-,-)] \\- [P(-,+,+) + P(-,+,-)] $$ $$C_{01} + C_{12} - C_{02} = 1 - 4[P(+,-,+) + P(-, +, -)]$$

Legget-Garg Inequality

$$C_{01} + C_{12} - C_{02} \leq 1$$

QM, qubit: $1.5$

QM, maximum: $3$

Budroni, Emary, PRL (2014)

MR ⇒ LGI

… but not the other way

LGI cannot detect every violation of MR, see later

Joint Probability

$$P(Q_0, Q_1, Q_2)$$

Let's call it

$$P_{012}(Q_0, Q_1, Q_2)$$

Measurements matter!

$$P_{12}(Q_1, Q_2) \neq P_{012}(Q_1, Q_2)$$

No-signaling in time

$$P_{2}(Q_2) = P_{12}(Q_2) = \sum_{Q_1'} P_{12}(Q_1', Q_2)$$

Kofler, Brukner, PRA (2013)

Here: NSIT(1)2

More NSITs

$$\text{NSIT}_{(0)1}:~P_{1} = P_{01}$$ $$\text{NSIT}_{(1)2}:~P_{2} = P_{12}$$ $$\text{NSIT}_{(0)2}:~P_{2} = P_{02}$$ $$\text{NSIT}_{0(1)2}:~P_{02} = P_{012}$$ $$\text{NSIT}_{(0)12}:~P_{12} = P_{012}$$

Trivial: Arrow of time

$$\text{NSIT}_{0(1)}:~P_{0} = P_{01}$$ $$\text{NSIT}_{0(2)}:~P_{0} = P_{02}$$ $$\text{NSIT}_{1(2)}:~P_{1} = P_{12}$$ $$\text{NSIT}_{01(2)}:~P_{01} = P_{012}$$

Revisiting LGI

$$C_{01} + C_{12} - C_{02} \leq 1$$ $$C_{01} \rightarrow C_{01(2)}$$ $$C_{12} \rightarrow C_{(0)12}$$ $$C_{02} \rightarrow C_{0(1)2}$$

LGI from NSIT

$$C_{01} + C_{12} - C_{02} \leq 1$$ $$\text{AoT}:~P_{01} = P_{012}$$ $$\text{NSIT}_{(0)12}:~P_{12} = P_{012}$$ $$\text{NSIT}_{0(1)2}:~P_{02} = P_{012}$$

Maroney, Timpson (2014)

We've only used 2,3
joint probabilitites

What about the
other NSITs?

NSITs
⇕
macrorealism012

NSIT(1)2 + NSIT0(1)2 + NSIT(0)12 + AoT ⇔ MR012

Example

qubit / Mach-Zehnder
interferometer

Mixed initial states $P(+) = q$.

Mach-Zehnder Interferometer

$R_1 = R_2 = \frac{1}{2}$ $R_1 = \frac{1}{4}, R_2 = \frac{3}{4}$
$\text{LGI}_{012}$ $1 + 3 \cos \varphi \geq 0$
$\text{NSIT}_{(1)2}$ $q = \frac{1}{2}$ or $\varphi = \frac{n\pi}{2}$ $q = \frac{1}{2}$ or $\varphi = \frac{n\pi}{2}$
$\text{NSIT}_{0(1)2}$ $\varphi = \frac{n\pi}{2}$ $\varphi = \frac{n\pi}{2}$
$\text{NSIT}_{(0)12}$

What does NSIT
mean in practice?

NSIT(0)T

$$P_{\hat B}(b) = \operatorname{tr}(\hat B_b \hat U_T \hat \rho_0 \hat U_T^\dagger \hat B_b^\dagger)$$ $$\bar P_{\hat B|\hat A}(b) = \int \text{d}a\,\operatorname{tr}(\hat B_b \hat U_T \hat A_a \hat \rho_0 \hat A_a^\dagger \hat U_T^\dagger \hat B_b^\dagger)$$

NSIT(0)0

$$P_{\hat B}(b) - \bar P_{\hat B|\hat A}(b) = \int \text{d}a\,\operatorname{tr}([\hat A_a \hat B_b, \hat B_b \hat A_a] \hat \rho_0) = 0$$ $$\int \text{d}a\,[\hat A_a \hat B_b, \hat B_b \hat A_a] = 0$$

General NSIT(0)0

$$\forall \rho_0: \text{NSIT}_{(0)0} \Leftrightarrow \int \text{d}a\,[\hat A_a \hat B_b, \hat B_b \hat A_a] = 0$$

For projectors

$$\forall \rho_0: \text{NSIT}_{(0)0} \Leftrightarrow [\hat A_a, \hat B_b] = 0$$

NSIT(0)T

$$P_{\hat B}(b) = \operatorname{tr}(\hat B_b \hat U_T \hat \rho_0 \hat U_T^\dagger \hat B_b^\dagger)$$ $$\bar P_{\hat B|\hat A}(b) = \int \text{d}a\,\operatorname{tr}(\hat B_b \hat U_T \hat A_a \hat \rho_0 \hat A_a^\dagger \hat U_T^\dagger \hat B_b^\dagger)$$

define $\tilde B_b^T \equiv \hat U_T^\dagger \hat B_b \hat U_T$

General NSIT(0)T

$$\forall \rho_0: \text{NSIT}_{(0)T} \Leftrightarrow \int \text{d}a\,[\hat A_a \tilde B^T_b, \tilde B^T_b \hat A_a] = 0$$

For projectors

$$\forall \rho_0: \text{NSIT}_{(0)T} \Leftrightarrow [\hat A_a, \tilde B^T_b] = 0$$

We have a condition for
macrorealism of

measurements &
Hamiltonians

we would expect

Two groups of measurements

some fulfill NSIT pairwise

some don't

Classical measurements

fulfill NSIT0(0)
with each member of
a consistent, complete
reference set

Classical Hamiltonians

fulfill NSIT0(T)
with each pair of members of
a consistent, complete
reference set

A-priori choice of

Reference operators

Coarse-grained versions of
quantum measurement operators

Reference operators

  • Coarse-grained coherent states
  • Unsharp quadrature measurements
  • Coarse-grained Fock measurements
$$V = \int \text{d}b \sqrt{P_{\hat B}(b) \bar P_{\hat B|\hat A}(b)} \in [0,1]$$

Bhattacharyya 1943

Coherent states

$$\hat A_\alpha = |\alpha\rangle\langle\alpha|, \hat B_\beta = |\beta\rangle\langle\beta|$$ $$\hat \rho_0 = |\gamma\rangle\langle\gamma|$$ $$V(T = 0) = \frac{2 \sqrt 2}{3} \approx 0.943$$

Coherent state bins

Overlap for different bin sizes

blue: bin border, orange: center of bin

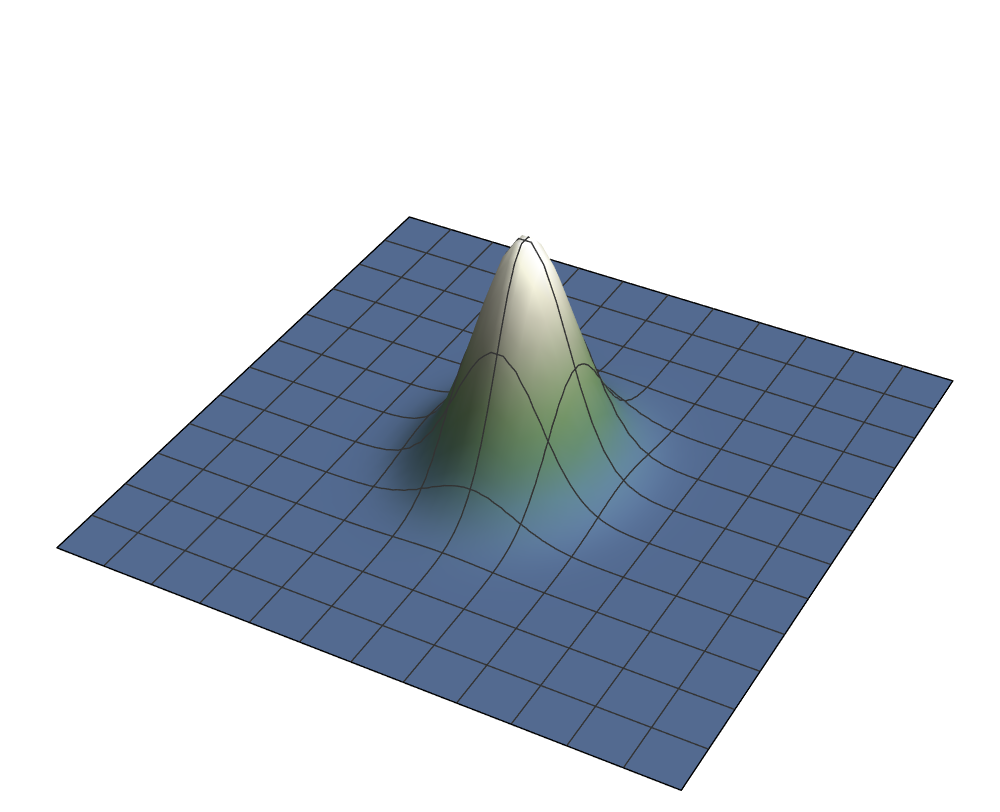
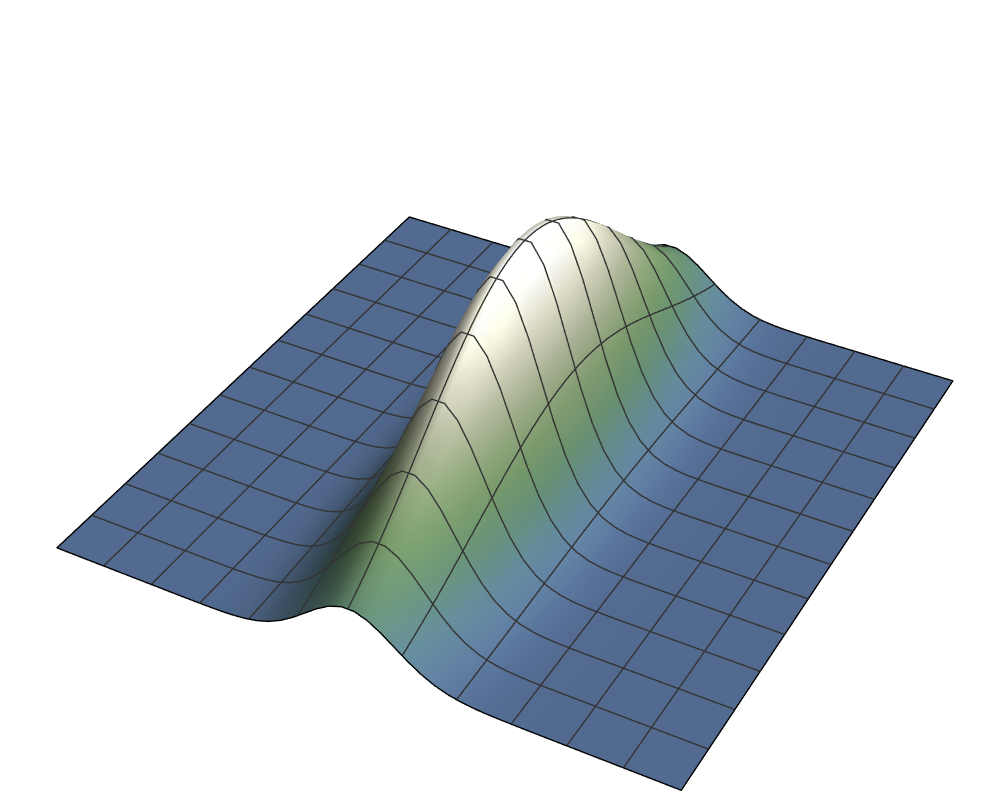
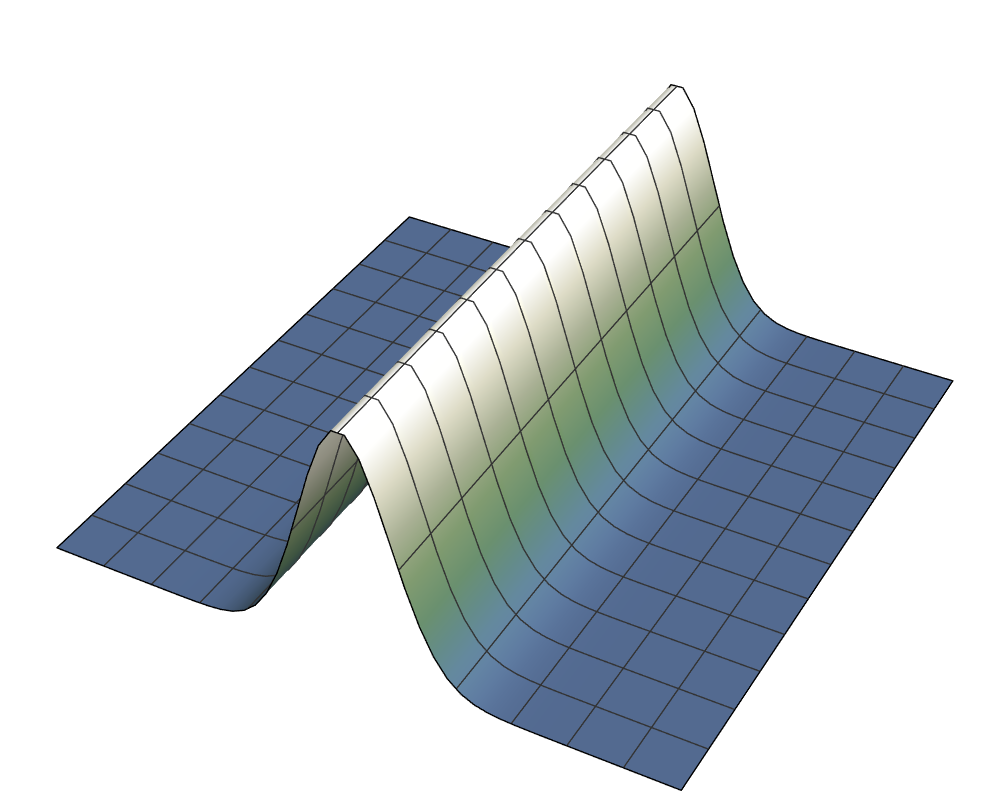$$V = 1 ~~~~~~~~~~~~~~~~ V \approx 0.67 ~~~~~~~~~~~~~~~~ V \approx 0.17$$

Probability distributions for quadrature measurements

left to right: increase in sharpness

Review

NSIT conditions for Macrorealism

NSIT for operators and Hamiltonians

Classicality

FIN