A primer to
Inflation
MPQ theory wednesday seminar by Lucas Clemente
clemente.io/inflation — github
2014-04-09
I'm not an expert!
Stuff will be wrong.
Please ask / correct me!


Image by NASA WMAP / Public Domain
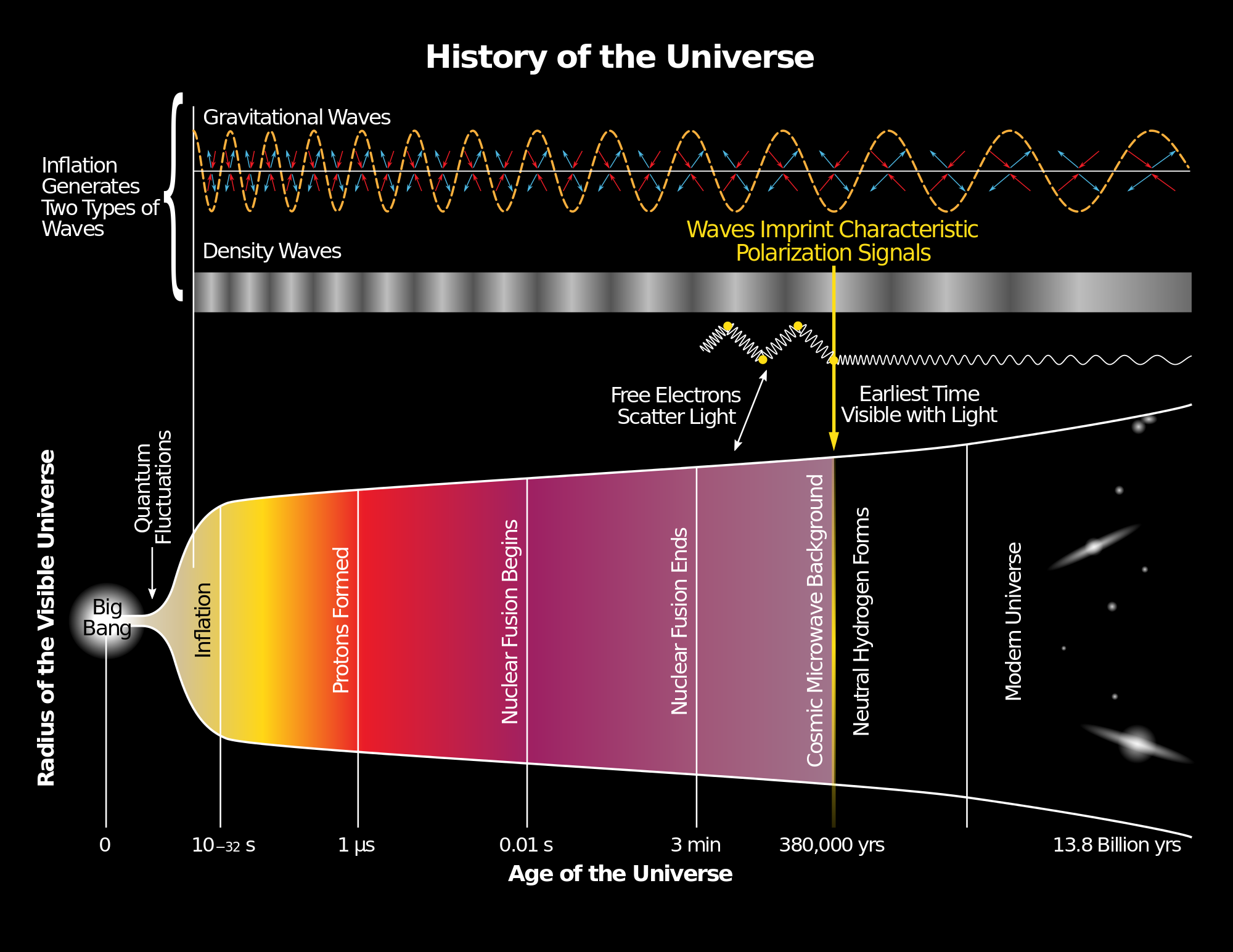
Image by Yinweichen / CC BY SA
Inflation
Fluctuations
Observation
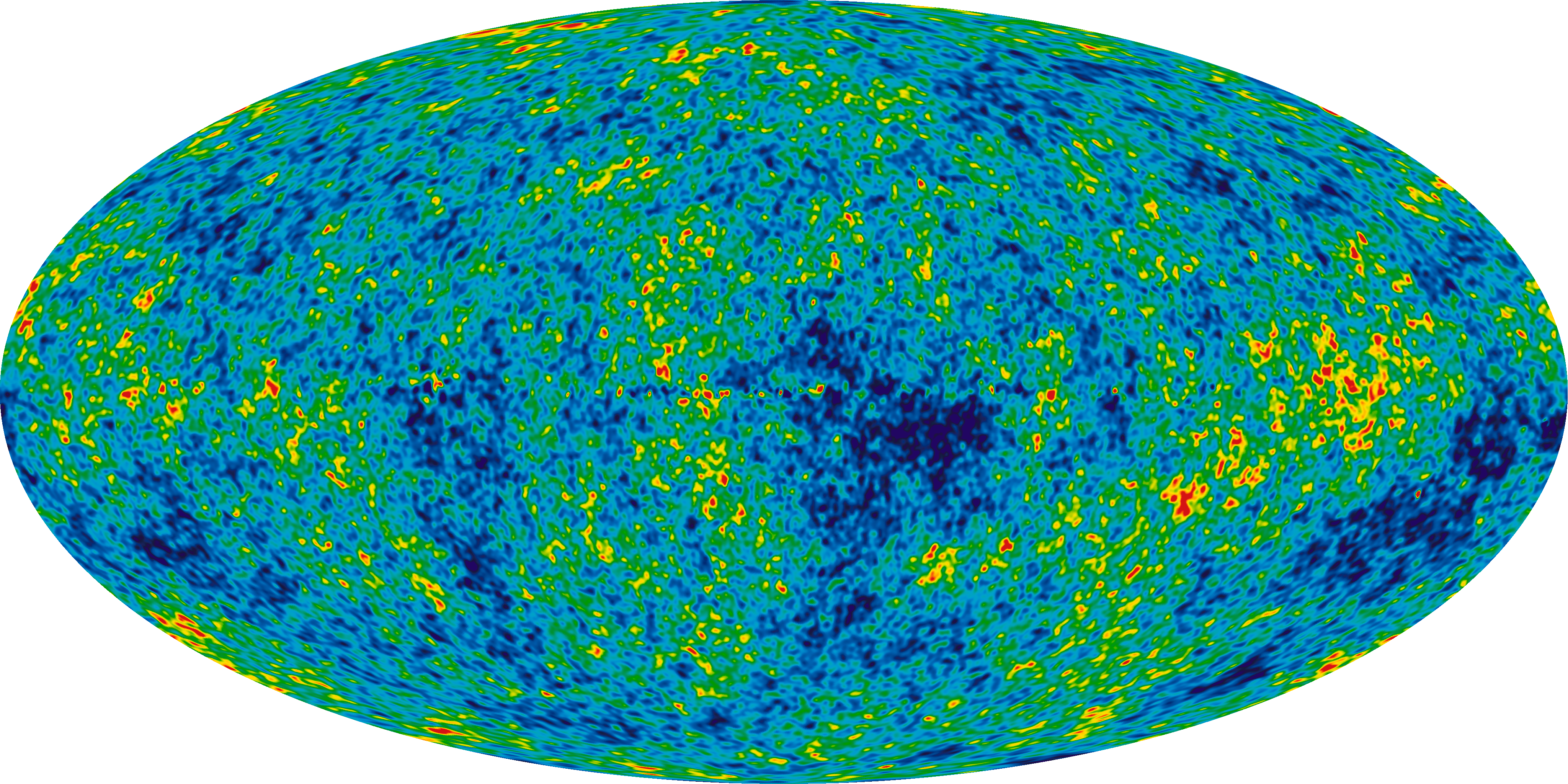
Cosmic Microwave Background (CMB)
Image by NASA / Public Domain
Problems:
Horizon
Flatness
Monopoles
Comoving coordinates
comoving observers see an isotropic universe / CMB
conformal time: time of comoving observers
comoving distance: constant between two comoving objects
FLRW Metric
$ds^2 = - dt^2 + a^2(t) (dx^2 + dy^2 + dz^2)$ scale factor $a(t)$, $a(\text{today}) \equiv 1$
$ds^2 = a^2(t) (- d\tau^2 + (dx^2 + dy^2 + dz^2))$
Hubble
Hubble's law: $v = H_0 D$
Hubble parameter $H = \frac{\dot a}{a}$
Hubble radius $(H)^{-1}$
comoving Hubble radius $(a H)^{-1}$
Three lengths
Radius of the observable universe $\tau$: 46 Gly
Age of the universe: 13.8 Gy
Hubble radius (today) $H_0^{-1}$: 14 Gly larger due to dark energy
Particle horizon
$\tau = \int d\tau = \int_0^t \frac{dt'}{a(t')} = \int_0^a (a' H)^{-1} d \ln a'$
maximum distance light can have travelled in time $t$
separation by ...
... comoving Hubble radius $(a H)^{-1}$: can't talk now
... comoving horizon $\tau$: could never have talked
different types of universe
decelerating universe: $(a H)^{-1}$ growing
accelerating universe: $(a H)^{-1}$ decreasing
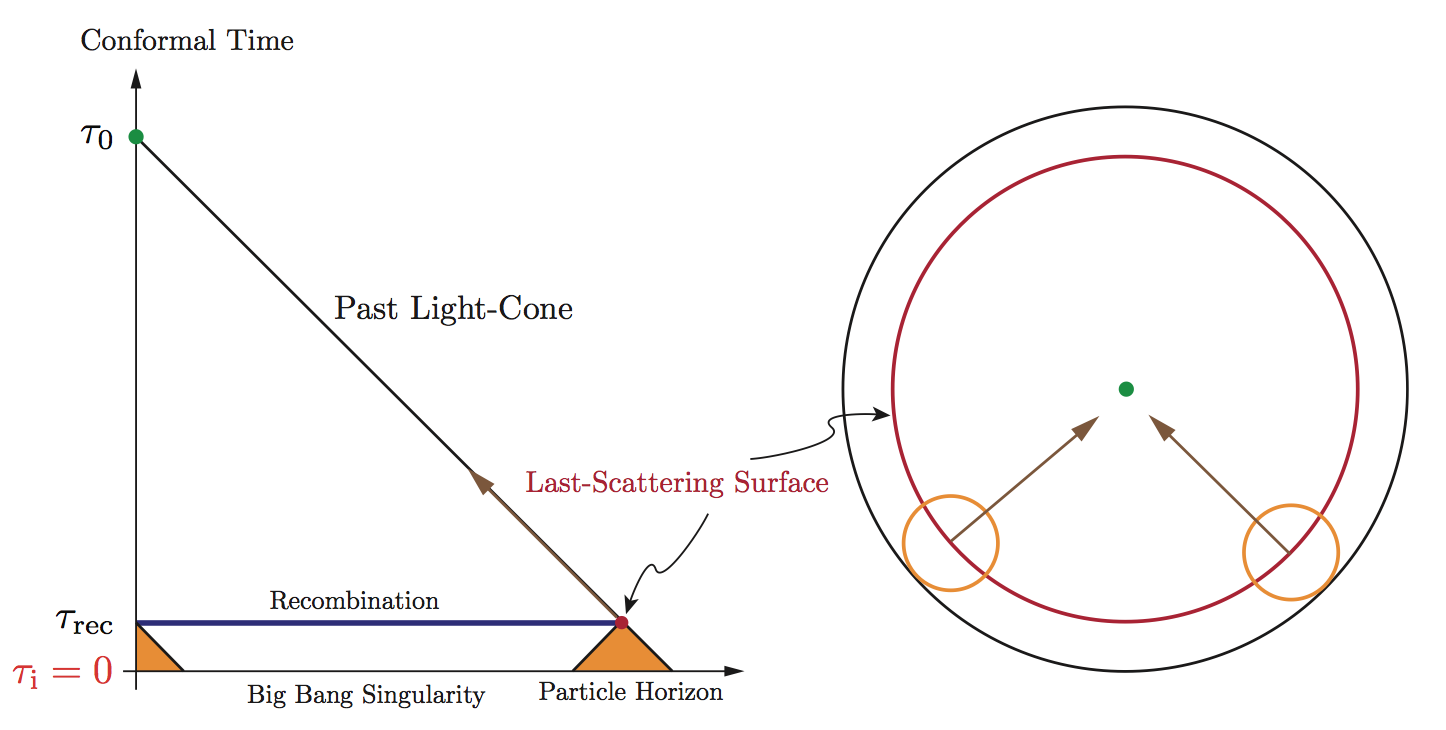
Image by Daniel Baumann / arXiv:0907.5424
Horizon Problem
If $(a H)^{-1}$ grows in time...
... stuff entering the comoving Hubble volume today
cannot have been in contact before!
... but the CMB is in thermal equilibrium!
Curvature of space
Friedmann Equation: $H^2 = \frac 1 3 \rho(a) - \frac{k}{a^2}$ where $k$: curvature (flat is $k=0$)
$1 - \frac{\rho(a)}{\rho_c(a)} = 1 - \Omega(a) = - \frac{k}{(aH)^2}$
Critical density: ~5 hydrogen per m3 Ordinary matter: ~0.2 per m3, rest is "dark"
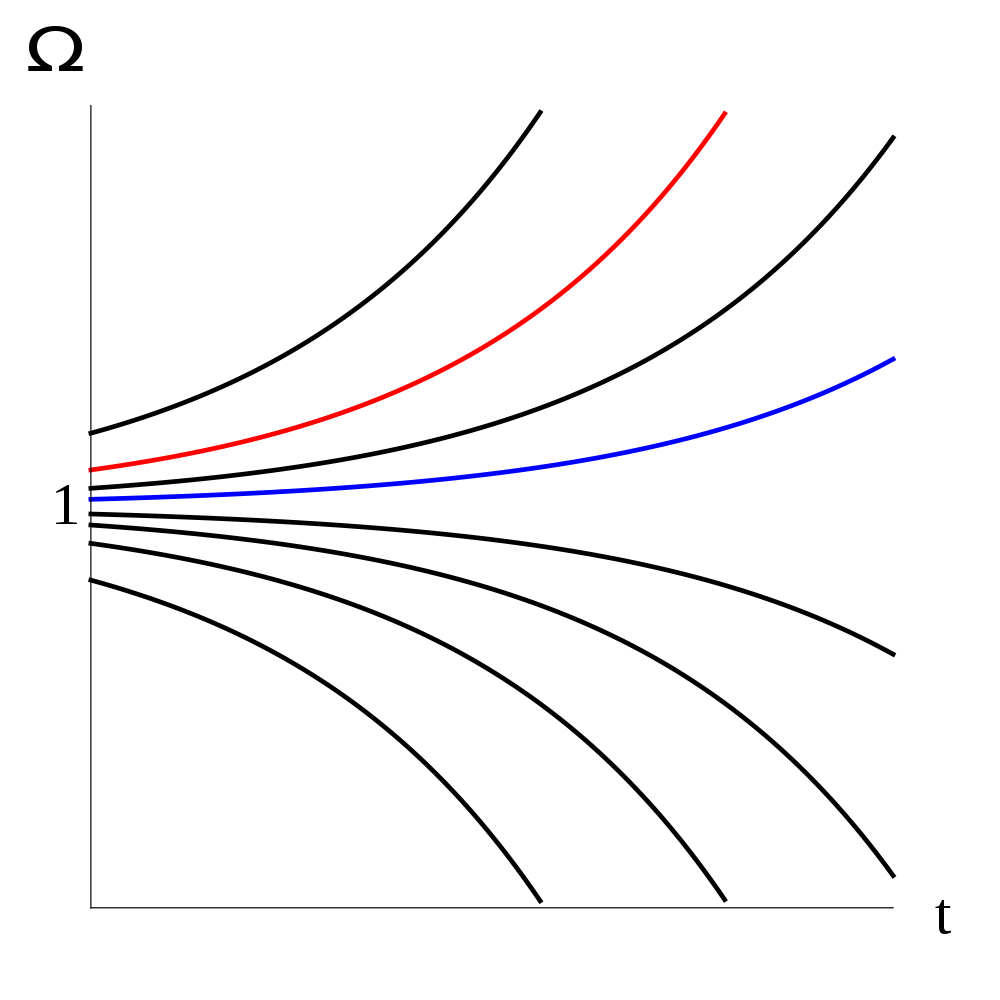
Image by Olaf Davis / Public Domain
Flatness Problem
$1-\Omega$ must have been fine tuned
to $~10^{-62}$ in Planck era!
Enter inflation
a decreasing comoving Hubble radius
Alan Guth, 1980
Inflation
comoving Hubble radius decreases $d_t (aH)^{-1} < 0$ Hubble radius $H^{-1}$ is constant
scale factor increases $\ddot a > 0$

Image by Andrew Liddle

Image by Daniel Baumann / arXiv:0907.5424
Horizon problem
solved
At CMB formation,
observable universe was
causally connected
Flatness problem
solved
$1 - \Omega(a) = - \frac{k}{(aH)^2}$
flat universe is attractor
Inflation
Fluctuations
Observation
Slow-roll inflation
Andrei Linde, 1982
Inflaton field $V(\phi)$
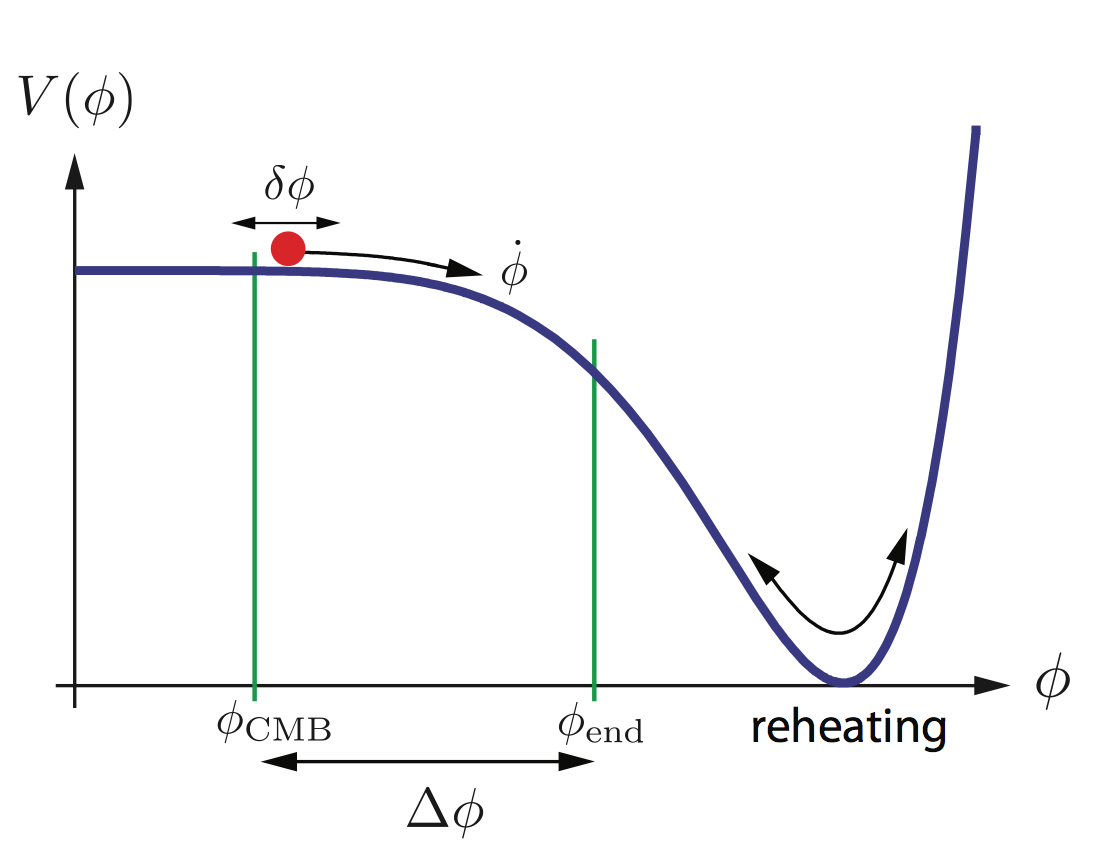
Image by Daniel Baumann / arXiv:0907.5424
Slow-rolling inflation
Friedmann equation $H^2 = \left(\frac{\dot a}{a}\right)^2 = \frac{V(\phi)}{3 m_P}$
If $\phi$ is slow-rolling, $V(\phi) \sim const$,
then $a(t) \sim e^{H t}$ inflates.
Quantum fluctuations
inflaton field fluctuates with wavelength $\lambda \sim e^{Ht}$
freezes in once $\lambda \sim (a H)^{-1}$
$\delta \phi \sim H$
Scalar and tensor fluctuations
energy density: $\delta_S^2 = \frac{1}{m_P} \frac{V^3}{V'^2}$
gravitational waves: $\delta_T^2 = \frac{V}{m_P^4}$
E- and B-modes
fluctuations imprint polarization onto CMB
scalar fluctuations ($\delta_S$): curl-free (E-modes)
tensor fluctuations ($\delta_T$): curl (B-modes)
BICEP2
$r = \frac{\delta_T^2}{\delta_S^2} = 0.2 \substack{+0.07\\-0.05}$
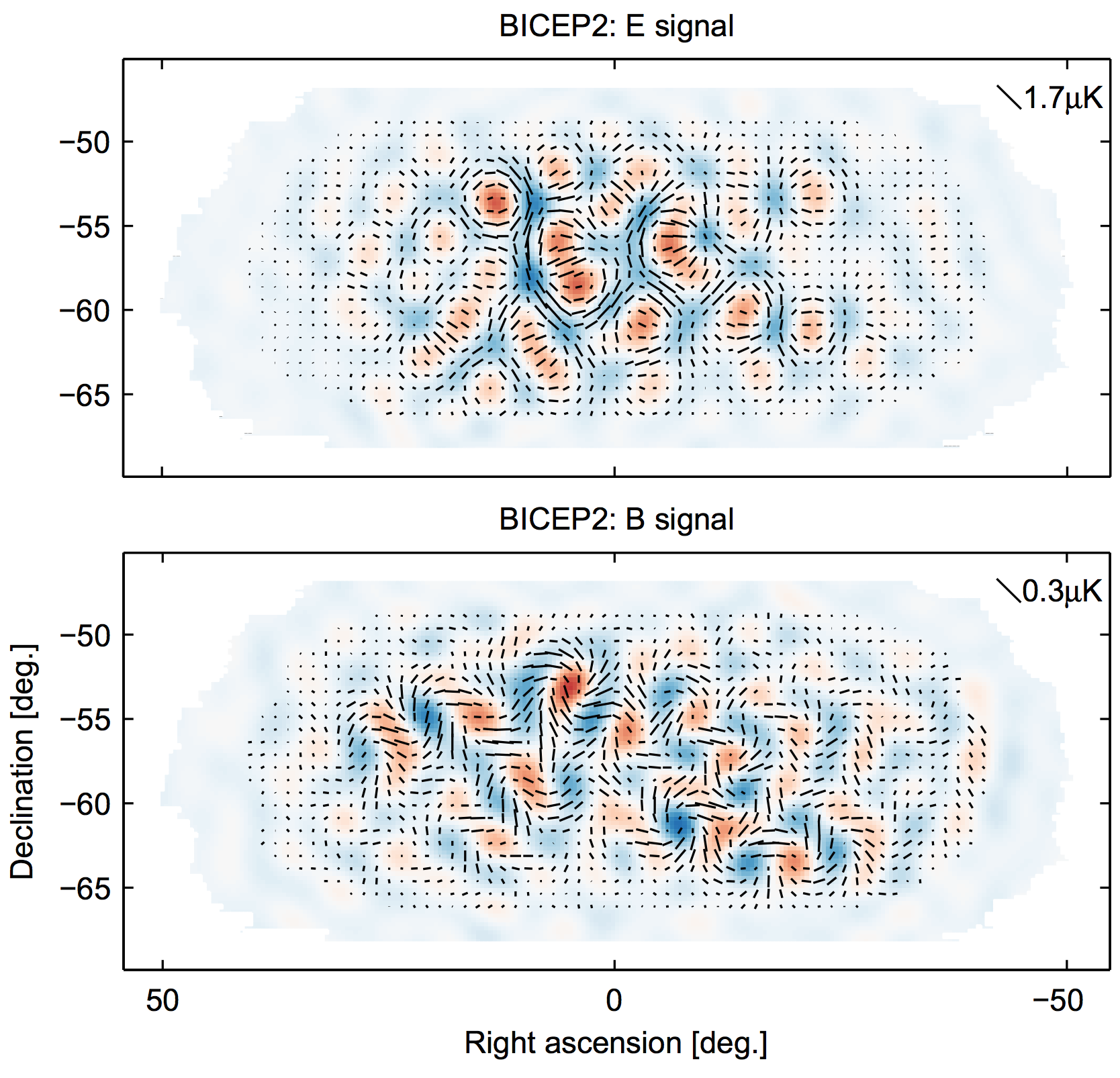
Image by BICEP2 / arXiv:1403.3985
planck scale
$r = 0.2$ allows determining $V \sim 10^{16} \text{GeV}$
reminder that $m_P \sim 10^{19} \text{GeV}$
inflation is close to the Planck-scale
where we could expect GUT effects
Inflation
Fluctuations
Observation

Photo by ESA
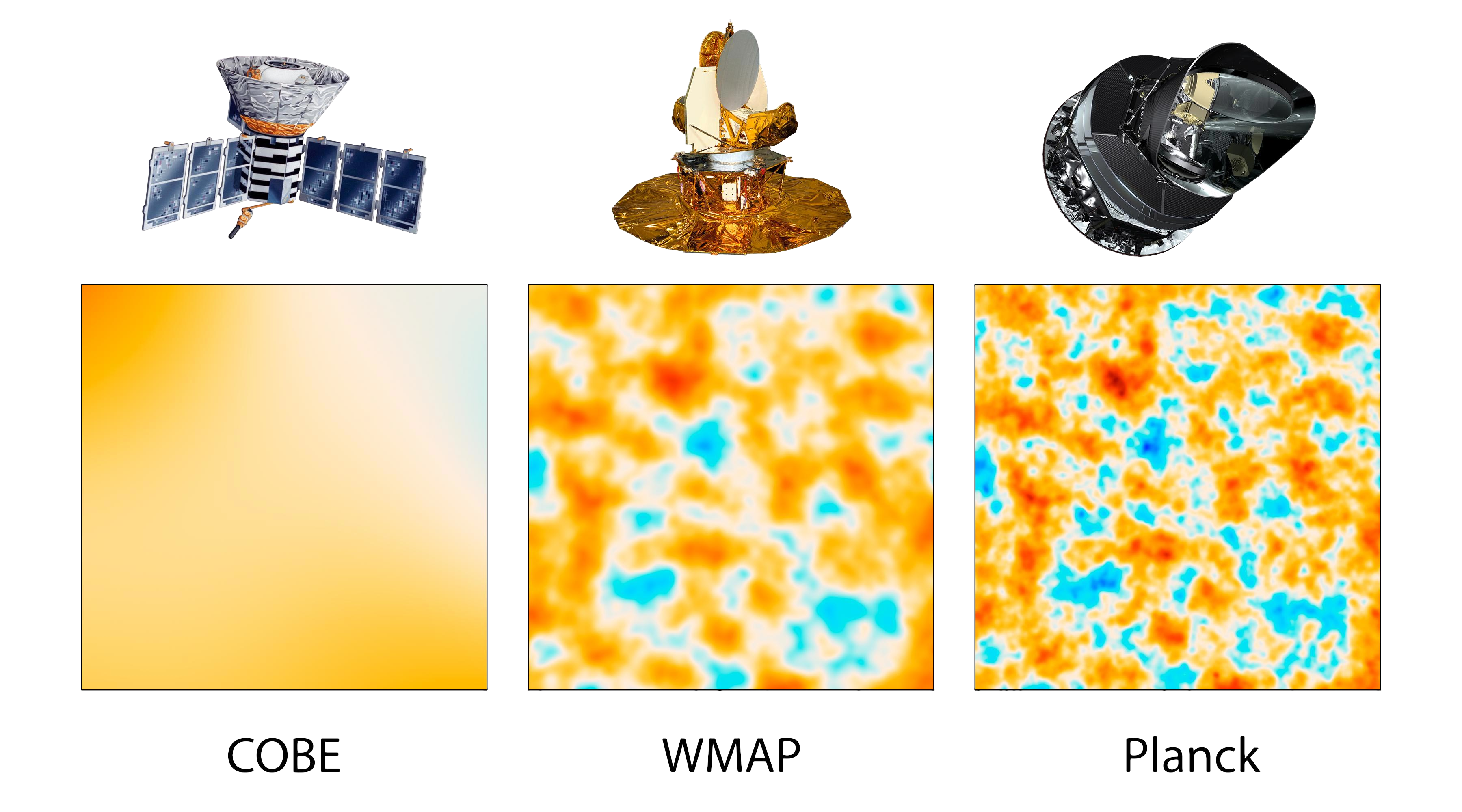
Image by NASA / Public Domain

Photo by Amble / CC BY SA

Photo by NASA / Public Domain
Links & References
TRICEP (Science, 04/14)
Tachyonic Retrospective Inferences of Cosmologically Extrapolated Preconditions
"... used a telescope outfitted with a revolutionary $11 million detector knitted out of individual superconducting carbon nanotubes, paid for in part by Google and the Roman Catholic Church."
predicted by Einstein in a dream on April 1st 1938!
THE END
questions?
once again, clemente.io/inflation